Week 8: Impressions on Week 7: Binary Trees

Hello,

Last week we learned about binary trees. Binary trees are just like tree but instead of having any number of children, binary trees only have two (left child and right child). I learned some pretty neat applications of binary trees that I never thought would be possible with trees:

Arithmetic Expression Trees:

What is puzzled me when I was a young programmer in grade 10 was how to represent data that  required special ordering in mathematical expressions. This is when I was trying to program a scientific calculator and it was not working out because I did not know how to represent data such as [(4 + (3 * 7)) - (5 / (3 + 4)] + 6.
But learning binary trees last week helped me understand that we can break this bigger problem in to sub problems and evaluate it in a tree. If we understand that each arithmetic operator (+, -, *, /) takes two inputs and has one output we can represent this in a node. Where the value of the node is its operator and its children can either be numbers or outputs of other operator nodes. This makes the problem shown above alot easier to represent on a computer and evaluate.

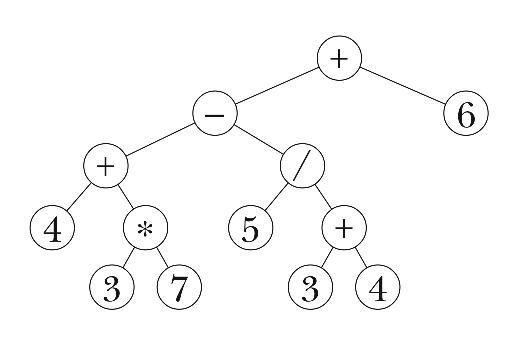
 Binary Search Trees:Another useful function of binary trees are making them function as a binary search tree. When I say binary search tree this means that for every node in the tree its left node is less than the node value and its right node is greater than the  node value. Why is formatting the tree in this way useful? Well if you want to search for a number in the tree instead of checking every value from start to end (linear search). For example if we wanted to search for 7 in the tree below we make an algorithm that does the following:- if node value is equal to 7 return true- if node value is less than 7 recursively check the right child- if node value is greater than 7 recursively check the left childDoing this will make the search MUCH faster than looking through every element. This will make you find the by just following a branch of the tree. In fact this seach runs in big omega of log n. Where linear search is n run time.  So these are two examples of how binary trees are really useful. This is the main thing I learned last week.   Thanks for reading,Rod Mazloomi